多角形の外角 1つの三角形の内角 の和は 180° 図6で示されるように, n角形は n−2 個の三角形に分けられるから,内角の和は (n−2)×180° 辺の数 3 4 5 n 形 三角形 四角形 五角形 n角形 内角の和 180° 360° 540° (n−2)×180° 図 6 問題 1 1 x の大きさを求めなさい x= ° 採点 消す Help (外角三角形の内角 三角形の内角の和は \(180°\) である。 内角とは、内側の角のことですね。 三角形の \(3\) つの内角の大きさをすべて、足すと \(180°\) 、つまり一直線になるということです。 三角形がどんな形であっても成り立ちます。 この事実は当然の丸暗記なのですが、なぜ?三角形の内角と外角 中学校数学では、主に円、三角形、四角形について学習します。2年生では三角形と四角形を主に学習します。まずは、三角形から調べてみましょう。 三角形の3つの内角(図形の内側の角)の和はいくつになるでしょうか。ここでは
数学老师手抄版 初二数学 三角形内角与外角 经典题 三角形内角与外角 内角 外角 新浪新闻
三角形 内角 外角 問題
三角形 内角 外角 問題-外角定理(がいかくていり)とは、三角形において2つの内角の和は隣り合わない1つの外角と等しい事を示す定理。 その形状から、「スリッパの法則」と呼ばれることもある 要出典 。 証明 三角形abcにおいて、内角の各々を∠a、∠b、∠cと表記し、辺bcをc側に延長した線上に点pをとり∠cの動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru


図形の扉 三角形の外角の定理
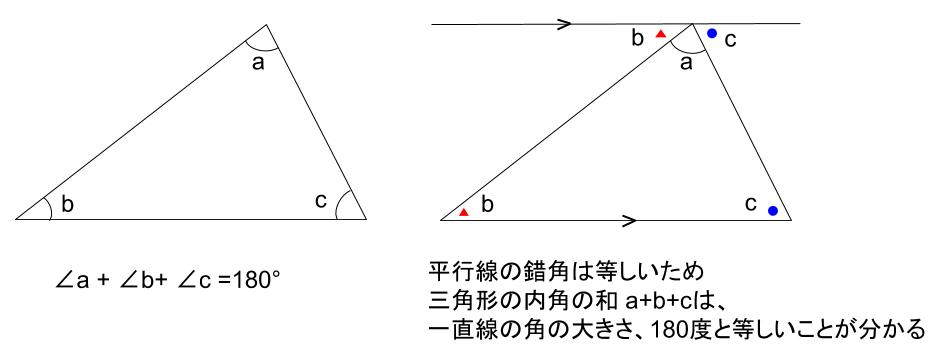
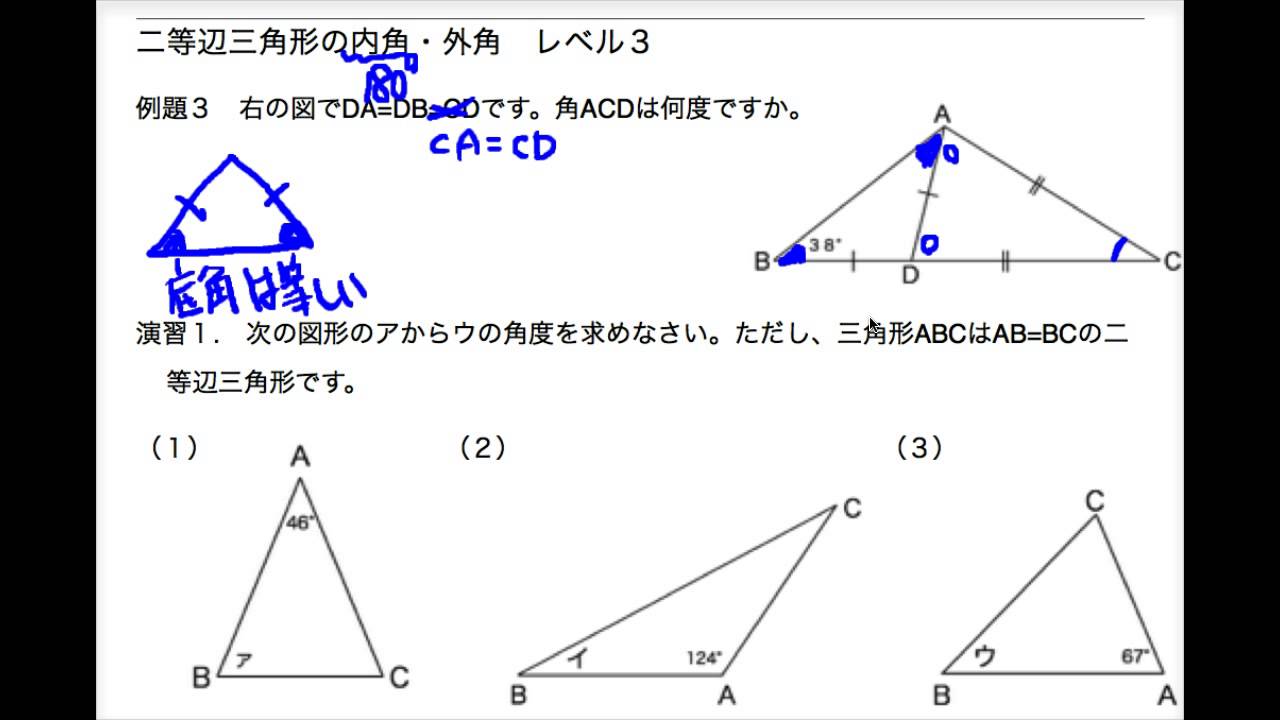
三角形の角度の問題です。 基本的なことを理解して、いろいろな問題を解いてみましょう。 余裕があれば難し目の応用問題にもチャレンジしてみてください。 三角形の内角の和は180° 三角形の内角の和は180°になります。 *ど図 1 でいえば、∠abc が内角の 1 つとなる。三角形は 3 つの内角をもち、その和は平面上では2直角( 180 度)となる(本稿はユークリッド幾何学における三角形を論じる)。 また、∠acd のように 1 つの辺と他の辺の延長との間にできる角を三角形の外角という。三角形・四角形の内角と外角 この錯角の性質を使うと 平行 a+b+c=180° になります。 つまり a +b+c=180°とは、 ∠A+∠B+∠C=180° 扌
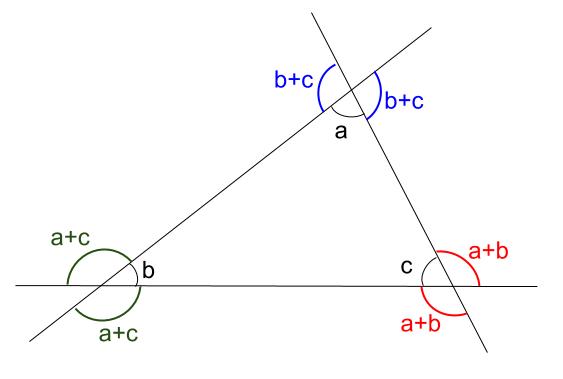
三角形の内角と外角の関係 三角形の1つの外角は,それととなり合わない2つの内角の和に等しくなります。これを示す意味で,注目する角の頂点から,その対辺に平行な補助線を引いています。 静止画 e1gai2jpg 600×400、 973KB 中学数学 ⇒ 平行と合同三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます.多角形の内角の和・外角の和の公式 多角形の内角の和と外角の和の公式をまとめると以下の通り。 N角形の内角の和:180°× (N −2) 180 ° × ( N − 2 ) 多角形の外角の和:360° 360 ° 内角の和は三角形の180°から、角が増えるごとに180°ずつ増えていきます。 それに対し、外角の和は角が増えても変わらず常に360°です。
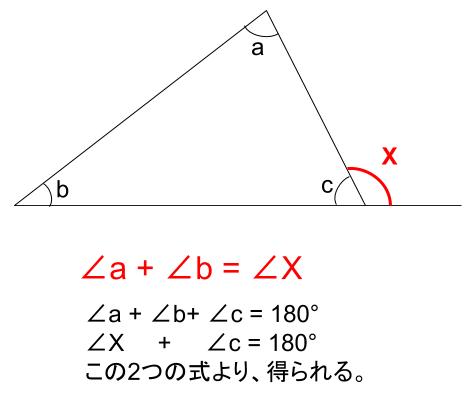
鋭角三角形の定義は、3つの全ての内角が90°以下なので この三角形は、鋭角三角形になります。 (2) は ③ 内角が 25° 48° 残りの内角は、107° になります。 鈍角三角形の定義は、三角形のどの角よりもわ小さくない角が、90°よりも大きい。 なので、この三角形は鈍角三角形になります。 ⑶ は ② 内角62° 28° 残りの内角は90°になります。 直角三角形の定義は、1つ三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます.三角形の3つの内角の和は180°になる。 三角形の外角 内容 三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。 証明a 図のように、 abcの辺bcを延長した直線上の点をdとする。 また、点cを通り辺baに平行な直線をceとする。



三角形的外角和是多少度 你搜我答


三角形的内角与外角会怎么考 老教师说有四个常考题型 来看看 内角 外角 三角形 新浪新闻
外角定理(がいかくていり)とは、三角形において2つの内角の和は隣り合わない1つの外角と等しい事を示す定理。 その形状から、「スリッパの法則」と呼ばれることもある 要出典 。 証明 三角形abcにおいて、内角の各々を∠a、∠b、∠cと表記し、辺bcをc側に延長した線上に点pをとり∠cのよって、三角形の内角をすべて足したら180°になることから $$x=180(7070)=40°$$ となります。 外角が与えられた場合には そこをたどって、二等辺三角形の内角を求めていくと 答えに近づくことができますね(^^)「多角形の外角の和」は、 なに角形でも(三角形でも十二角形でも)360°です。 だから正十二角形のひとつの外角は、 360°÷12=36°となります。 よって、正十二角形のひとつの内角は、 180°36°=144°となります。



9 2 三角形内角和外角 1 参考课件 共10张ppt Ppt 豆知网


三角形外角 三角形外角定理 三角形外角和 三角形的外角
内角と外角を足すと180°になる という特徴があります。 これを使って考えると 正多角形の内角1つ分の大きさは $$\large{180(外角)}$$ このように求めてやることができます。 正三角形の場合三角形の外角の性質 内角の隣にある外側の角のことを 外角 といいます。 外角の大きさは、 隣にない内角2つの和 に等しくなります。三角形の内角と外角の関係 三角形の外角は、 それと隣り合わない2つの内角の和に等しい。 という定理がありますがちょっと見方を変えるとよりはっきり分かります。 まず、 「直線の角度は180度」 です。 そして、 「三角形の内角の合計は180度」 です。 (角A)+(角B)+(角C)=180度 そして 以上のことを利用し、外角にとなり合わない2つの内角を下の図の


初一奥数第18讲三角形内角和经典例题 2 雪花新闻



三角形内角外角图片 第1页 一起扣扣网
三角形の外角の定理 『外角は、その外角のとなり以外の2つの内角の和に等しい』 つまり、下の図の通り。 外角の定理のひみつ外角= + ①三角形の内角の和は180度でした。 だから、 + + =180度角というのは、直線や線分が交差した点と、その両端の線で挟まれた部分のことを言います。 多角形はどのように区別がされているかというと、この角の数によってされています。 左から「三角形」「四角形」「五角形」です。 また、図形の内側の角を 内角 といい、それから延長した辺と1辺がつくる角を 外角 といいます。 この2つの角度を足すと 180° になり三角形の内角と外角の関係 三角形の1つの外角は,それととなり合わない2つの内角の和に等しくなります。これを示す意味で,注目する角の頂点から,その対辺に平行な補助線を引いています。 静止画 e1gai2jpg 600×400、 973KB 中学数学 ⇒ 平行と合同


三角形内角与外角的解题误区 5 4三角形的内角和 初中湘教版 数学中国网


三角形的内角和推论8 Id拂晓犬吠 博客园
三角形の内角の和は 180 ° 180 ° なので、 60 ° 70 ° ∠ C = 180 ° ① 60 ° 70 ° ∠ C = 180 ° ① ※ ∠ C ∠ C は内角を表すことにする。 また、一つの内角と外角の和は 180 ° 180 ° なので、 ∠ C ∠ x = 180 ° ② ∠ C ∠ x = 180 ° ② ①②より、 ∠ x = 60 ° 70 ° = 130 ° ∠ x = 60 ° 70 ° = 130 ° (証明1終了) 「三角形の内角の和が180度である」 ことを三角形の内角の和は180°なので、∠xを求めると 40°75°∠x=180° → ∠x=65° 外角と∠xの和は、180°(直線だから)なので、 ∠外角=180° 65°=115° ・・・(答え)さらに三角形の外角の性質を利用すると このように、\(2x\)の大きさになっている角を見つけることができます。 次は、\(∠2x\)を含む二等辺三角形に注目 最後は一番大きな二等辺三角形に注目と流れていきます。 すると、大きな二等辺三角形の内角はそれぞれ\(x, 2x, 2x\) と表すことができまし


利用三角形内角外角性质解决角度问题 哔哩哔哩 つロ干杯 Bilibili


三角形的一个外角等于与它不相邻的两个内角和 这个怎么理解 求图 求例题 作业 慧海网
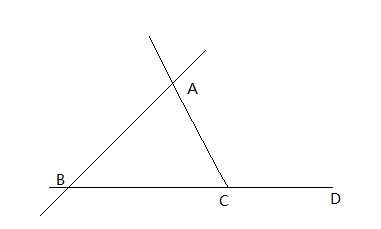
となり,このことから,「三角形の3つの内角の和は180°」ということがわかります。 また, ∠acd=∠ace∠ecd=∠a∠b より,「三角形の1つの外角は,その隣にない2つの内角の和に等しい(外角の定理)」ということもわかります。 例題三角形の内角と外角の性質は次の $2$ つとなります。 ① 三角形の内角の和は $\textcolor{blue}{180°}$ である ② 三角形の外角は、それととなり合わない $\textcolor{blue}{2}$ つの内角の和に等しい まずは、① 三角形の内角の和は $180°$ である について、なぜそうなるのか確認しましょう。三角形の内角と外角の関係について 三角形の内角と外角の関係は角度を求める問題でよく使うので、 しっかり理解しておく必要があります。 三角形の内角の性質 三角形の内側にある3つの角のことを「内角」という。 この3つの内角の和は必ず180°になる。



3 三角形外角定理 简书


図形の扉 三角形の外角の定理
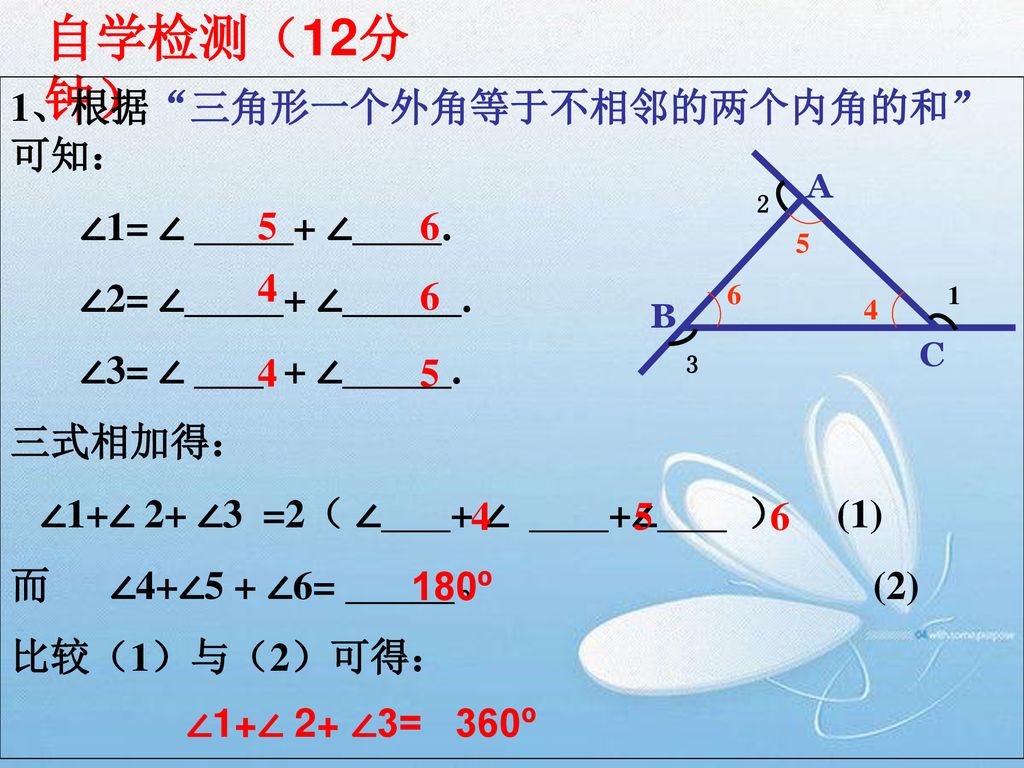
三角形の内角と外角 解説 多角形の1辺と,その1辺と隣り合う辺の延長とが作る角を外角といい,多角形の隣り合った2辺が作る,多角形の内側に向いた角を内角といいます。 次の図のように, abcの辺bcを延長した直線上に点d,辺acを延長した直線上に点eをとります。 このとき,∠acd,∠bce三角形・四角形の内角と外角 この錯角の性質を使うと 平行 a+b+c=180° になります。 つまり a +b+c=180°とは、 ∠A+∠B+∠C=180° 扌高校講座・学習メモ 三角形・四角形の内角と外角 これは、どんな図形にもいえることで、 四角形の場合も、 (∠Aの外角)+(∠Bの外角)+(∠Cの外角)+(∠Dの外角) =360° つまり、外角の和は1つの図形の周りを1周することと同じなので、360°になります。


数学老师手抄版 初二数学 三角形内角与外角 经典题 三角形内角与外角 内角 外角 新浪新闻



教师资格证面试 小学数学真题教案设计 知乎
三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます.動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru


2 三角形的内角与外角和 Page76 华师大版七年级数学下册电子课本 教材 教科书 好多电子课本网
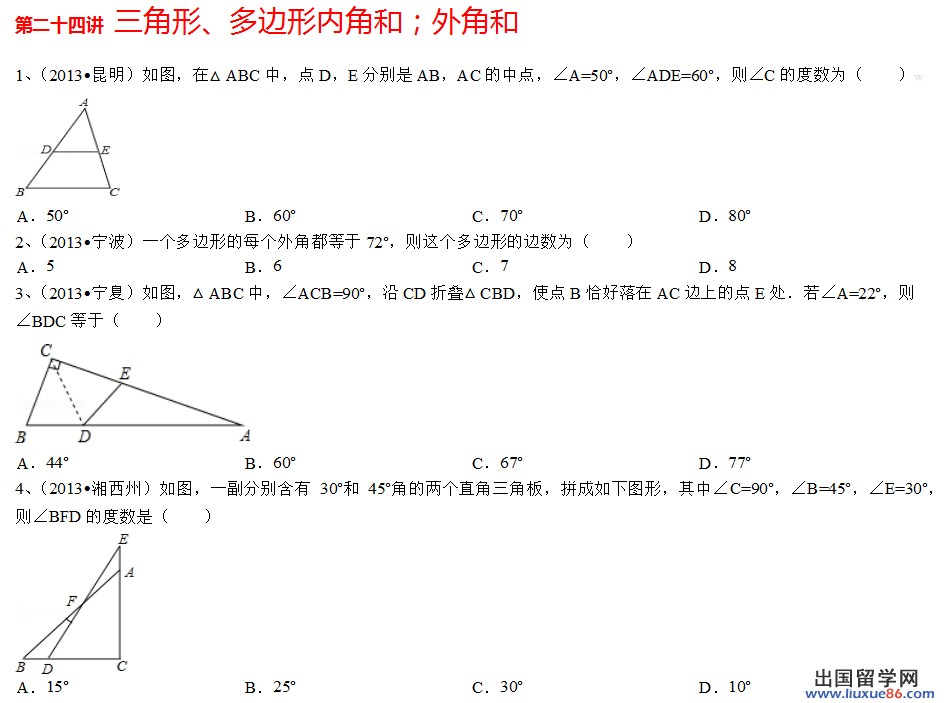


14初三数学三角形多边形内角和外角和



初中统考几何相似三角形 内角平分线与外角平分线的性质 老雷数学 Youtube


三角形的内角和外角 Ppt下载 第一ppt


数学老师手抄版 初二数学 三角形内角与外角 经典题 三角形内角与外角 内角 外角 新浪新闻
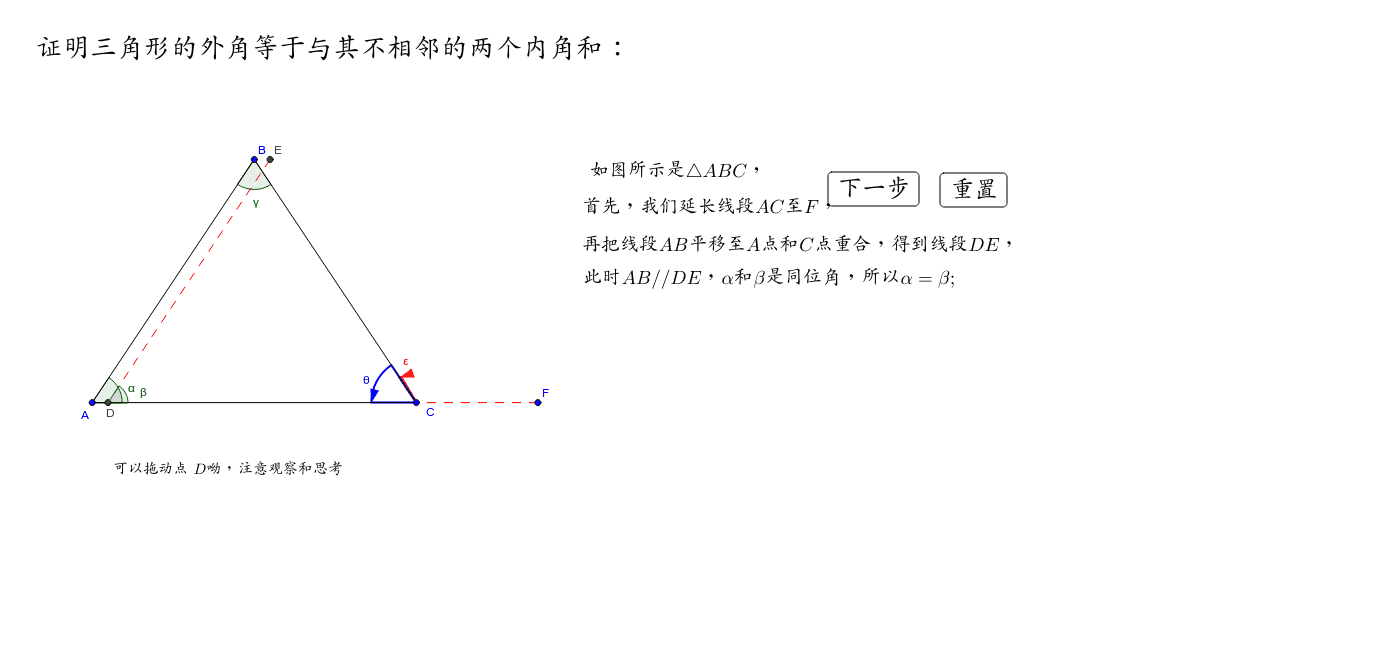


三角形的外角等于与其不相邻的两个内角之和 Geogebra


中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



初一奥数第18讲三角形内角和经典例题 1 每日头条



多边形的内角



三角形内角外角定理多边形 三角形png图片素材免费下载 图片编号 Png素材网



八年级数学上册第七章平行线的证明5三角形内角和定理第2课时与三角形外角有关的定理优秀教案 北师大版 莲山课件



内角和外角 维基百科 自由的百科全书


中考数学三角形与多边形ppt精品课件 图文 百度文库


初中数学与三角形有关的角 掌握考点 明确考法 学会解题思路 看点快报


中考命题或命题真假的判断


霸姐数学 初二上册 三角形的内角 外角 第二讲 哔哩哔哩 つロ干杯 Bilibili


三角形的内角和外角 Ppt下载 第一ppt


中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



93多边形的内角和和外角和3 Ppt课件 文库吧


第七章平行线的证明三角形内角和定理 Ppt Download


三角形一个内角与一个外角的角平分线夹角的度数初中数学八年级上册 哔哩哔哩 つロ干杯 Bilibili


课件 教员分享 Z1版 七年级数学 沪教版 八年级下 22 1 探索多边形的内角和 免费数学课件下载 优思教辅


三角形的内角和定理 外角的性质 07年中考题集锦 第34周 7 1 7 2 初中人教五四制 数学中国网



原本 1 16 三角形的外角大于任意不相邻的内角 求证 每日头条


三角形的外角讲解 北京爱智康
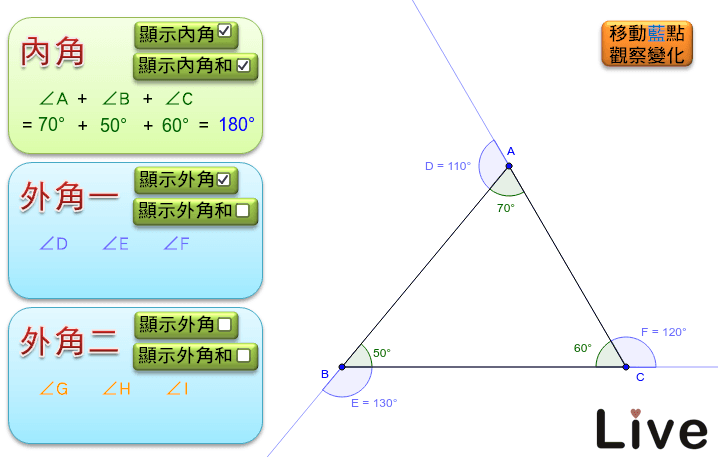


三角形的內角 外角 內角和與外角和 Geogebra



对多边形对角线 内角和 外角和的理解 Geogebra


中学数学 三角形の内角と外角の関係の利用


三角形外角 三角形外角定理 三角形外角和 三角形的外角



三角形内角外角平分线的夹角五个模型



初二4 2 三角形的内角与外角 Youtube


11 2 2 三角形的外角 人教版八年级上册数学电子课本 数九网


初中数学每日一题 221 巧用外角 简化计算 1 三角形内角 外角性质



多边形的内角和与外角和 简书
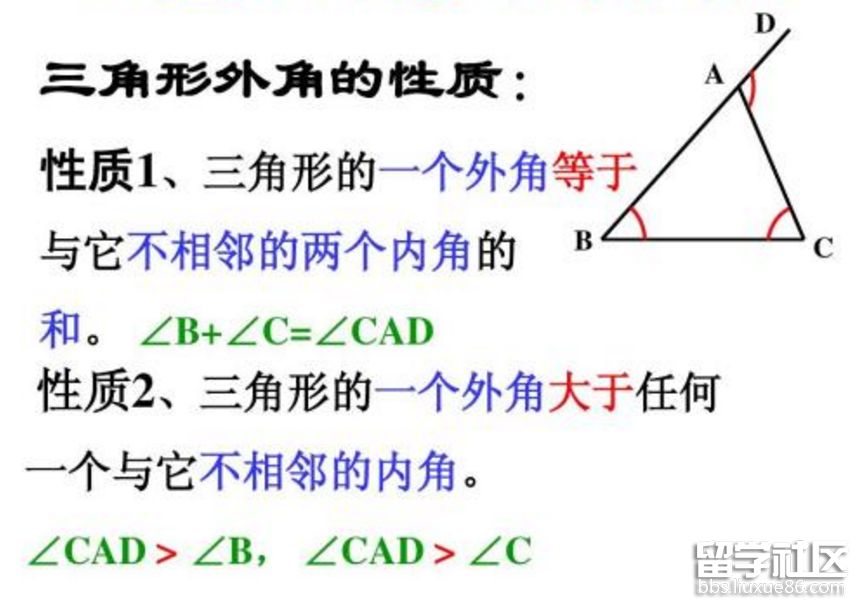


中考数学 三角形 考点 与三角形有关的角


图解名校初中数学压轴题 几何3 1 利用三角形内角和定理及推论计算角度或证明角的相等关系



中2数学 三角形の内角と外角 例題編 映像授業のtry It トライイット


三角形的外角1 主题阅读 我爱图谱 知识图谱 思维导图 Www 5itupu Com



三角形外角练习模板 三角形外角练习文档下载 金锄头文库 手机版



Xmeducation 中小学补习学院 10秒了解三角形内角和 外角和的理论 Facebook
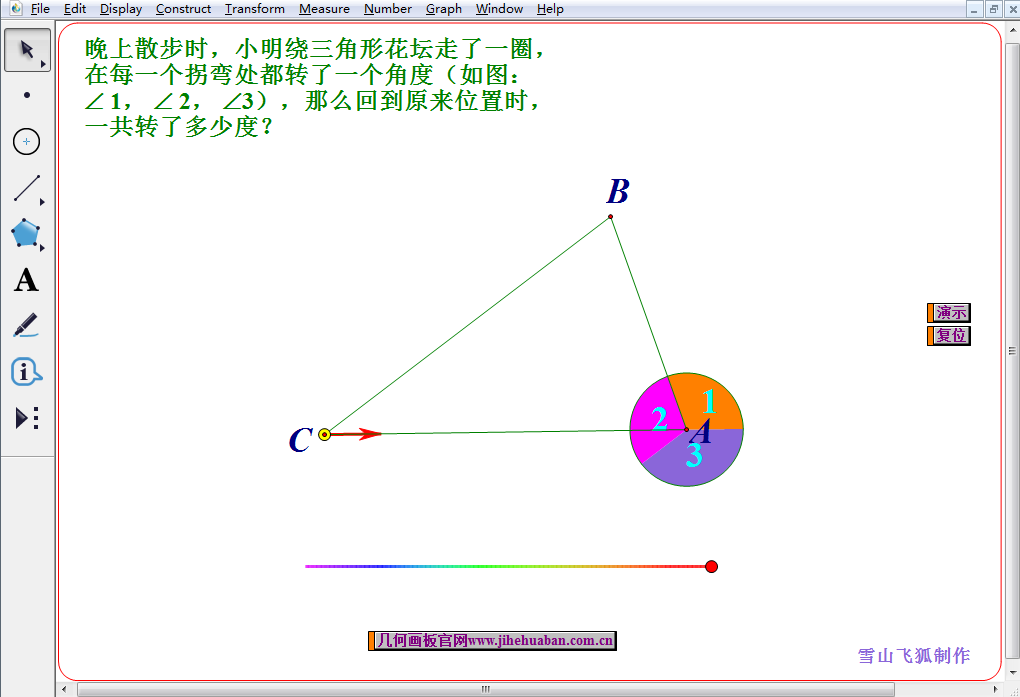


三角形外角和的证明三角形外角和6种证明方法
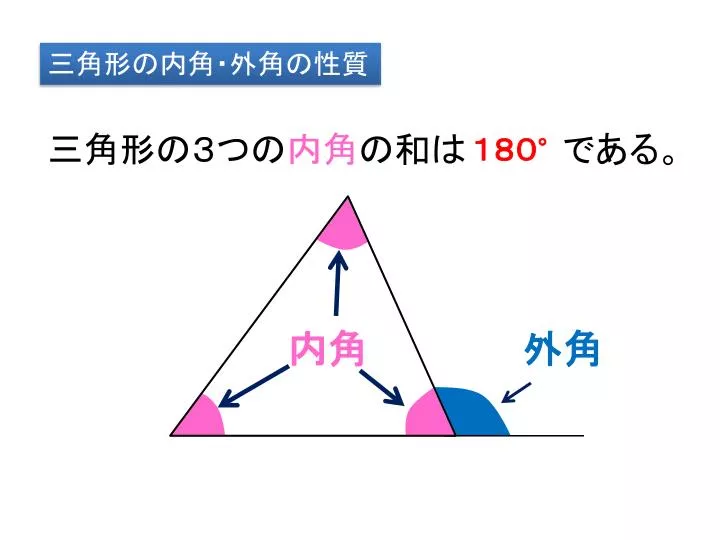


Ppt 三角形の内角 外角の性質 Powerpoint Presentation Free Download Id



三角形内角外角图片 第1页 一起扣扣网



三角形内角外角图片 第1页 一起扣扣网


悟空问答 如何反驳学生认为三角形有六个外角 26个回答


课件 教员分享 Z1版 七年级数学 沪教版 八年级下 22 1 探索多边形的内角和 免费数学课件下载 优思教辅


数学老师手抄版 初二数学 三角形内角与外角 经典题 三角形内角与外角 内角 外角 新浪新闻



三角形内角外角图片 第1页 一起扣扣网


数学老师手抄版 初二数学 三角形内角与外角 经典题 三角形内角与外角 内角 外角 新浪新闻


外角公式 内角和公式和外角和公式 正多边形外角和公式 正n边形的内角和公式



多边形外角和和内角和的关系 三人行教育网 Www 3rxing Org


三角形的内角和外角 Ppt下载 第一ppt



外角公式 内角和公式和外角和公式 正多边形外角和公式 正n边形的内角和公式


初中数学每日一题 221 巧用外角 简化计算 1 三角形内角 外角性质


三角形内角和是多少度 外角和度数是多少 初三网


三角形元素外角定理内角三角形png图片素材免费下载 图片编号 Png素材网



画像をダウンロード三角形内角外角


数理天地


Word版 巧用三角形的外角以及三角形内角和公式的变形来解决三角形中角的有关求解与证明 7 2与三角形有关的角 初中人教版 数学中国网



数学 中2 48 三角形の内角と外角 基本編 Youtube


三角形外角定理 腾讯视频
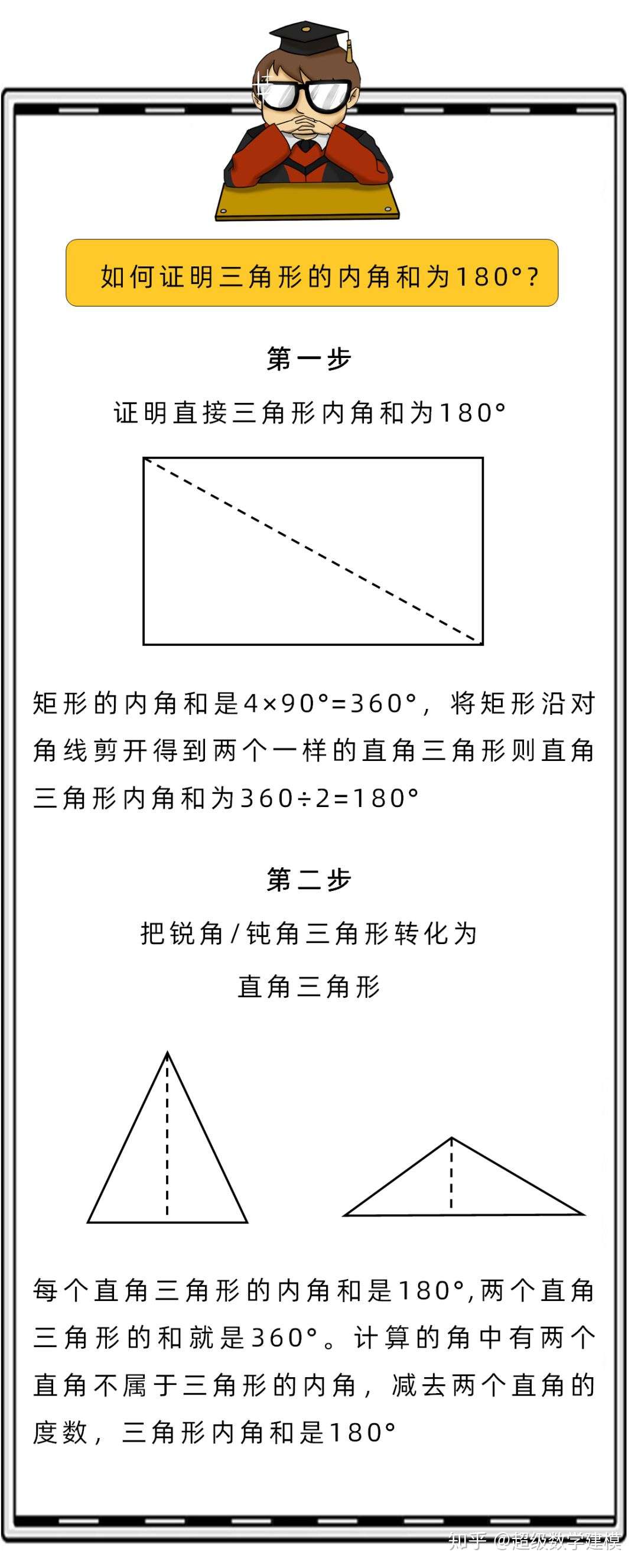


陈省身 三角形内角和不等于180 知乎
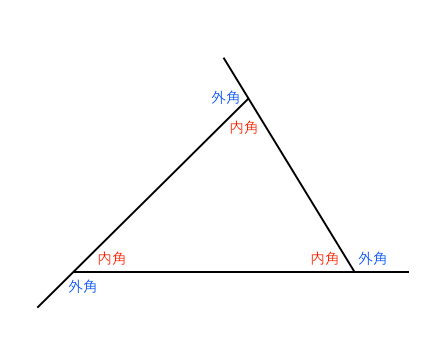


三角形外角 三角形外角定理 三角形外角和 三角形的外角
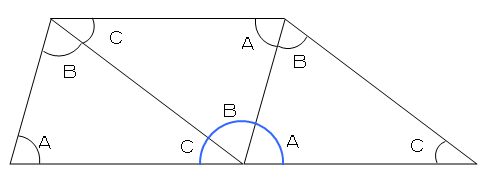


三角形の内角と外角の関係



八年级数学上册第七章平行线的证明5三角形内角和定理第2课时与三角形外角有关的定理优秀教案 北师大版 莲山课件


三角形内角和是多少度 外角和度数是多少 初三网



多边形的内角


三角形的外角等于与它不相邻的两个内角的和 Page18 浙教版八年级 初二 数学上册电子课本 教材 教科书 好多电子课本网


考点19 三角形的外角与内角和定理4 邱亮老师工作室



File 三角形の内角と外角 Png 维基百科 自由的百科全书


8 2 2 三角形的外角 一 A 备课吧


第1周周末卷三角形内角 外角 文档之家


通俗数学 三角形外角和等于360 优胜于 内角和等于180 职业数学家在民间 微信公众号文章阅读 Wemp



多边形的内角和与外角和 简书



探究神奇的几何世界 相关定理合集第一部分 网易订阅
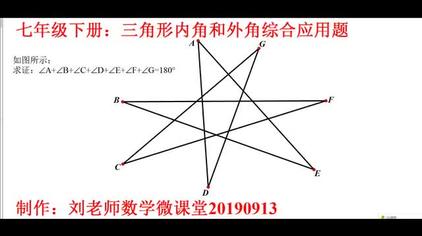


七角星的内角和怎么求 西瓜视频


数学老师手抄版 初二数学 三角形内角与外角 经典题 三角形内角与外角 内角 外角 新浪新闻



八年级数学每日一题第27集多边形内角与外角三角形内角和定理 最新高清视频在线观看 芒果tv



三角形两个外角的和等于第三个内角的4倍 则第三个内角等于 雨露学习互助



三角形内角外角平分线的夹角五个模型


7 2 2三角形的外角 备课吧
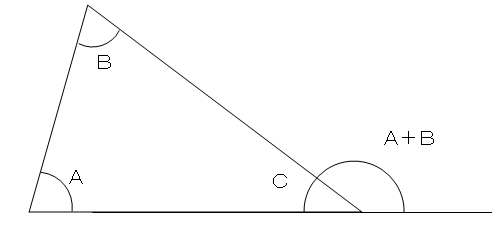


三角形の内角と外角の関係


三角形外角定理 腾讯视频


初二月考备考 三角形与全等三角形知识讲解 重点练习 附答案精讲 初中数学 微信公众号文章阅读 Wemp



9 1 2 三角形的内角和与外角和 参考课件2 共25张ppt Ppt 豆知网



八年级上册第十一章 三角形 简介



0 件のコメント:
コメントを投稿